降价策略下的利润优化 实现6080元目标

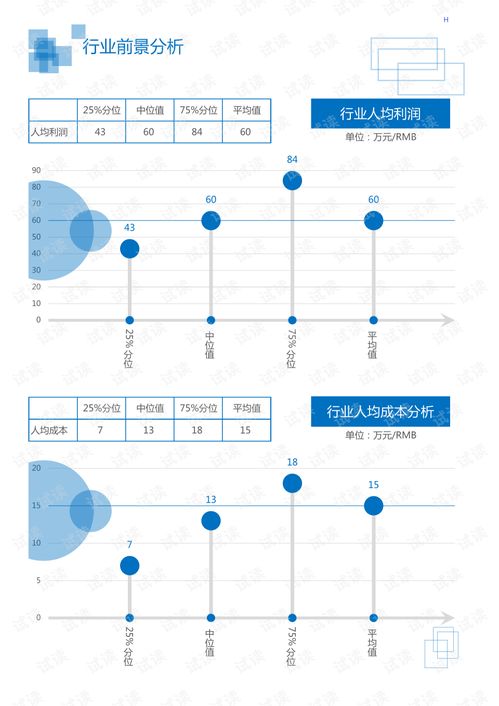
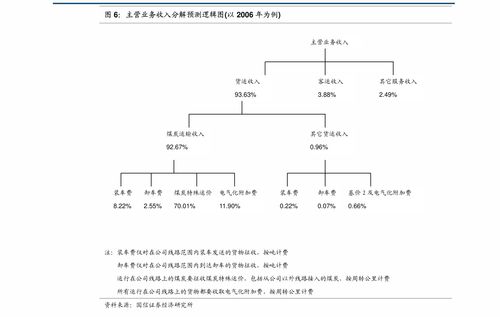
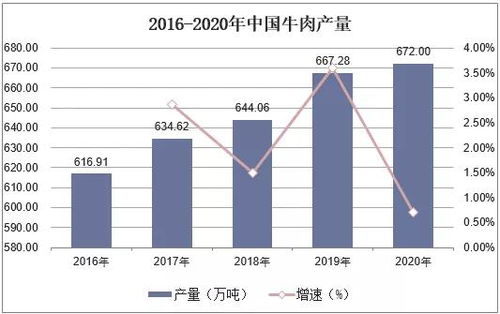
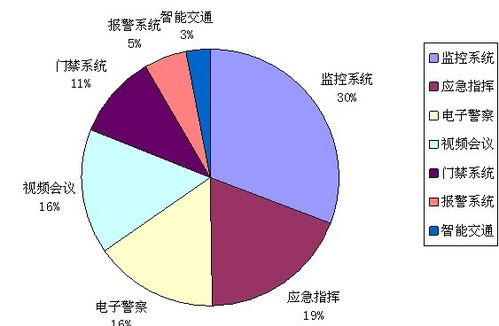
在当前市场环境下，某商品的售价为每件60元，每星期可卖出300件。市场调查显示，每降价1元，每星期可多卖出20件。商品进价为每件40元。商家希望在顾客得到实惠的前提下，即通过降价让消费者受益，同时实现6080元的利润目标。\n\n我们需要分析降价对销售量和利润的影响。设降价金额为 \( x \) 元（\( x \geq 0 \)），则新售价为 \( 60 - x \) 元，每星期销售量变为 \( 300 + 20x \) 件。每件商品的利润为售价减去进价，即 \( (60 - x) - 40 = 20 - x \) 元。因此，总利润 \( P \) 可表示为：\n\[ P = (20 - x)(300 + 20x) \]\n\n商家目标利润为6080元，因此我们需要解方程：\n\[ (20 - x)(300 + 20x) = 6080 \]\n展开并整理得：\n\[ 6000 + 400x - 300x - 20x^2 = 6080 \]\n\[ 6000 + 100x - 20x^2 = 6080 \]\n\[ -20x^2 + 100x - 80 = 0 \]\n两边除以-20简化：\n\[ x^2 - 5x + 4 = 0 \]\n解这个二次方程：\n\[ (x - 1)(x - 4) = 0 \]\n所以 \( x = 1 \) 或 \( x = 4 \)。\n\n在顾客得到实惠的前提下，降价应尽可能大，让消费者受益更多。因此，我们选择 \( x = 4 \) 元。此时，新售价为 \( 60 - 4 = 56 \) 元，每星期销售量为 \( 300 + 20 \times 4 = 380 \) 件。验证利润：\n\[ P = (20 - 4) \times 380 = 16 \times 380 = 6080 \] 元，符合目标。\n\n结论：商家应将售价降至56元每件，这样每星期可卖出380件，在顾客享受4元降价实惠的同时，商家能获得6080元的利润。市场调研支持了这一策略的有效性，显示了价格弹性对销售量的积极影响，同时平衡了利润目标与消费者利益。